Condução de Calor Transiente Bidimensional

Introdução

O estudo de caso apresentado aqui, a condução de calor transiente em uma placa bidimensional, tem um papel interessante, pois ele não é exatamente o objetivo deste texto, mas sim um meio. Deixe-me explicar, dia desses me deparei com Xarray (formalmente xray), pacote Python que se destina a tornar o trabalho com arranjos de dados multidimensionais uma tarefa simples, eficiente e divertida.

Xarray introduz rótulos na forma de dimensões, coordenadas e atributos sobre os dados brutos dos arranjos em formato NumPy, permitindo uma experiência de desenvolvimento mais intuitiva, consistente e a prova de falhas.

Após ler a documentação oficial, fiquei empolgado para ver como esse pacote funciona na prática, e fico feliz em compartilhar essa experiência com você. Aqui entra o estudo da condução de calor transiente bidimensional, que será descrito a seguir. Logo após, o problema será resolvido com estruturas de dados NumPy, para contextualizar o leitor com três abordagens diferentes, e então, o mesmo problema será resolvido com Xarray para comparação.

# Como sempre, o primeiro passo é importar
# os pacotes que vamos utilizar

# NumPy para manipulação de arranjos N-dimensionais
import numpy as np

# Matplotlib para graficar os resultados
import matplotlib.pyplot as plt

# Xarray, para testar o conceito dos rótulos
# na forma de dimensões, coordenadas e atributos
import xarray as xr

Descrição do Problema

Uma placa de cobre de \( (L_x \times L_y) = ( 50 ~ cm \times 50 ~ cm ) \) inicialmente possui temperatura em toda a sua extensão igual à \( T_0 = 0^oC \).

Instantaneamente, a temperatura em suas bordas é elevada. Vamos admitir que cada um dos contornos tenha uma variação linear de acordo com a temperatura definida nos vértices da geometria, conforme mostra a figura a seguir:

Sabe-se que as propriedades do material são:

• Condutividade térmica \( k = 52 ~ W/m \cdot K \);
• Calor específico \( c_p = 420 ~ J / kg \cdot K \);
• Massa específica \( \rho = 8.800 ~ kg / m^3 \);
• Difusividade térmica \( \alpha = k / (\rho c_p) \).

Considerando um passo de tempo $\Delta t = 4 ~ s$ e a resolução espacial de $\Delta x = \Delta y = 5 ~ cm$, calcule a evolução da temperatura na placa até o tempo de $6.000 ~ s$.

Equação bidimensional que define a difusão de calor:

\[ \dfrac{\partial T}{\partial t} = \alpha \left( \dfrac{\partial ^2 T}{\partial x^2} + \dfrac{\partial ^2 T}{\partial y^2} \right), \quad 0 \le x \le L_x, \quad 0 \le y \le L_y, \quad t \ge 0. \]

Condições de cortorno:

\[ T_{x0} = T(x=0,y) = y \dfrac{T_d - T_a}{L_y} + T_a, \] \[ T_{xn} = T(x=L_x,y) = y \dfrac{T_b - T_c}{L_y} + T_c, \] \[ T_{y0} = T(x,y=0) = x \dfrac{T_c - T_a}{L_x} + T_a, \] \[ T_{yn} = T(x,y=Ly) = x \dfrac{T_b - T_d}{L_x} + T_d. \]

Condição inicial:

\[ T(x,y) = T_0, \quad para \quad t=0. \]

Discretizando com a derivada segunda numa representação por diferença central e a derivada primeira com diferença ascendente temos:

\[ \dfrac{T^{n+1} _{i,j}-T^{n} _{i,j}}{\Delta t}=\alpha \left[ \dfrac{T^{n} _{i-1,j}-2T^{n} _{i,j}+T^{n} _{i+1,j}}{(\Delta x)^2} +\dfrac{T^{n} _{i,j-1}-2T^{n} _{i,j}+T^{n} _{i,j+1}}{(\Delta y)^2} \right], \quad 0 \le i \le I, \quad 0 \le j \le J, \quad n \ge 0, \]

\[ T_{x0} = y_j \dfrac{T_d - T_a}{L_y} + T_a, \quad para \quad i=0 \quad e \quad 0 \le j \le J, \] \[ T_{xn} = y_j \dfrac{T_b - T_c}{L_y} + T_c, \quad para \quad i=I \quad e \quad 0 \le j \le J, \] \[ T_{y0} = x_i \dfrac{T_c - T_a}{L_x} + T_a, \quad para \quad 0 \le i \le I \quad e \quad j=0, \] \[ T_{yn} = x_i \dfrac{T_b - T_d}{L_x} + T_d, \quad para \quad 0 \le i \le I \quad e \quad j=J, \] \[ T_{i,j}^n = T_0, \quad para \quad n=0. \]

Lembre-se que o critério de estabilidade numérica do problema é:

\[ \Delta t \le \dfrac{\Delta x^2}{4 \alpha}. \]

Desenvolvimento

Uma vez descrito o problema, partimos para a prática! No bloco de código a seguir definimos todos os parâmetros físicos e numéricos que necessitamos:

# Propriedades do Material
k = 52.0  # W/mK
cp = 420.0  # J/kgK
rho = 8800.0  # kg/m^3

# Temperatura nos vértices
Ta = 60.
Tb = 20.
Tc = 0.
Td = 100.

# Temperatura inicial
T0 = 0.

# Discretização espacial
x = np.linspace(start=0., stop=.5, num=21, endpoint=True)
y = np.linspace(start=0., stop=.5, num=21, endpoint=True)
# e temporal
t = np.linspace(start=0., stop=600., num=601, endpoint=True)

E então realizamos os primeiros cálculos:

# Cálculo da difusividade térmica
alpha = k / (rho * cp)

# Passo de tempo e resolução da malha ao quadrado
dt, dx2, dy2 = t[1] - t[0], (x[1] - x[0])**2., (y[1] - y[0])**2.

# Estabilidade numérica
if dt <= np.minimum(dx2, dy2) / 4. / alpha:
    print('Critério de estabilidade satisfeito.')
else:
    print('Atenção! Critério de estabilidade não satisfeito.')

Critério de estabilidade satisfeito.

Lembre-se que a documentação de qualquer função pode ser facilmente acessada sempre que surgir alguma dúvida sobre a sintaxe ou sobre os argumentos que ela aceita, basta digitar help(np.linspace).

A partir daqui começa a resolução do problema:

# Alocar a temperatura e impor condição inicial
T = T0 * np.ones((x.size, y.size, t.size))

# Condições de Contorno
Tx0 = (Td - Ta) / (y[-1] - y[0]) * y + Ta
Txn = (Tb - Tc) / (y[-1] - y[0]) * y + Tc
Ty0 = (Tc - Ta) / (x[-1] - x[0]) * x + Ta
Tyn = (Tb - Td) / (x[-1] - x[0]) * x + Td

# Aplicando as condições de contorno no tempo inicial
T[0, :, 0] = Tx0
T[-1, :, 0] = Txn
T[:, 0, 0] = Ty0
T[:, -1, 0] = Tyn

Bom, aqui fazemos uma observação quanto aos arranjos em NumPy, é preciso sempre ter em mente a maneira como foram definidos. No caso da temperatura temos três coordenadas na ordem [x, y e t], ou [i, j e n] no espaço discreto. Portanto, ao aplicar T[0,:,0] = Tx0, dizemos que T será igual à Tx0 onde i=0 e n=0, para todo o j, exatamente o que queremos para essa condição de contorno, o mesmo pode ser percebido nas demais superfícies. Lembre-se que em Python, o índice -1 retoma o último elemento de uma dada dimensão.

Vamos definir uma função auxiliar para graficar os resultados obtidos, assim podemos facilmente repetir a produção de figuras para as diversas abordagens que usaremos. Veja o código:

def minha_figura(T, x, y):
    fig, ax = plt.subplots(nrows=1, ncols=3, sharey=True, figsize=(12, 4))

    # Variação temporal da temperatura no centro da placa
    ax[0].plot(t, T[x.size // 2, y.size // 2, :])
    ax[0].set(xlabel='t [s]',
              ylabel=r'T [$^0C$]',
              title=f'x={x[x.size//2]} e y={y[y.size//2]}')

    # E duas figuras para variação espacial:
    nfigs = 5
    for n in range(nfigs):
        time = n * ((t.size) // (nfigs - 1))
        # Variação com x e t para y fixo
        ax[1].plot(x, T[:, y.size // 2, time], label=f't={t[time]}s')
        # Variação com y e t com x fixo
        ax[2].plot(y, T[x.size // 2, :, time], label=f't={t[time]}s')

    # Adicionamos alguns detalhes visuais
    ax[1].set(xlabel='x [cm]', title=f'y={y[y.size//2]}')
    ax[2].set(xlabel='y [cm]', title=f'x={x[x.size//2]}')

    ax[1].legend()
    ax[2].legend()

    plt.show();

NumPy

O avanço no tempo se dá ao isolarmos o termo \( T^{n+1} _{i,j} \) na equação governante discreta, que então assume a forma:

\[ T^{n+1} _{i,j} = T^{n} _{i,j} + \alpha \Delta t \left[ \dfrac{T^{n} _{i-1,j}-2T^{n} _{i,j}+T^{n} _{i+1,j}}{(\Delta x)^2} +\dfrac{T^{n} _{i,j-1}-2T^{n} _{i,j}+T^{n} _{i,j+1}}{(\Delta y)^2} \right], \]

para: \(\quad 0 \le i \le I, \quad 0 \le j \le J, \quad n \ge 0 \).

Perceba que quando n=0, todos os valores à direita da igualdade são conhecidos (nossa condição inicial), e assim, pode-se calcular o termo à esquerda, que será a temperatura em n+1. Repetindo esse processo sucessivamente para cada valor de i, j e n, atingimos qualquer valor de tempo desejado, passo à passo.

A maneira mais intuitiva de programar a equação acima é escrevê-la exatamente como ela é, percorrendo todo o espaço bidimensional e o tempo por meio de três laços aninhados, e aplicando as condições de contorno ao final de cada passo de tempo:

%%time
for n in range(t.size - 1):
    for i in range(1, x.size - 1):
        for j in range(1, y.size - 1):
            T[i, j, n + 1] = T[i, j, n] + alpha * dt * (
                (T[i - 1, j, n] - 2. * T[i, j, n] + T[i + 1, j, n]) / dx2 +
                (T[i, j - 1, n] - 2. * T[i, j, n] + T[i, j + 1, n]) / dy2)
    # Condições de contorno
    T[0, :, n + 1], T[-1, :, n + 1], T[:, 0,
                                       n + 1], T[:, -1,
                                                 n + 1] = Tx0, Txn, Ty0, Tyn

Wall time: 921 ms

E então graficamos o resultado:

minha_figura(T, x, y)

Note que no tempo nós já conhecemos a solução para n=0, então calculamos o laço temporal t.size-1 vezes. De maneira similar, a temperatura é conhecida em todas as paredes, então não precisamos resolver a equação nos contornos, e assim, cada laço temporal exclui a primeira e a última posição (range(1,x.size-1), por exemplo).

Embora o bloco de código acima resolva o problema, essa não é uma boa abordagem do ponto de vista do tempo necessário para o cálculo, ao realizar sequencialmente cada uma das operações por meio do aninhamento de laços.

Sobre NumPy, além do suporte para arranjos multi-dimensionais, toda a biblioteca é programada em C. Temos o desempenho de uma linguagem compilada (C), dentro de um ambiente de linguagem interpretada (Python), o melhor de dois mundos. Para tirar proveito disso, o ideal é realizar as operações vetorialmente ao resolver o problema em fatias (mais informações aqui), de modo que podemos reescrever o código como:

%%time
for n in range(t.size-1):
    T[1:-1,1:-1,n+1] = T[1:-1,1:-1,n] + dt * alpha * (
        (T[ :-2,1:-1,n] - 2. * T[1:-1,1:-1,n] + T[2:  ,1:-1,n]) / dx2 +
        (T[1:-1, :-2,n] - 2. * T[1:-1,1:-1,n] + T[1:-1,2:  ,n]) / dy2
    )
    # Condições de contorno
    T[0,:,n+1], T[-1,:,n+1], T[:,0,n+1], T[:,-1,n+1] = Tx0, Txn, Ty0, Tyn

Wall time: 21 ms

Vemos os resultados novamente com:

minha_figura(T, x, y)

Temos exatamente a mesma resposta para um tempo de cálculo inferior. Bem, esse ganho de desempenho depende das características da sua máquina e do problema, talvez podem nem ser perceptíveis quando usamos apenas 21 pontos em cada direção espacial, mas experimente aumentar esses valores.

Uma terceira alternativa com NumPy é deixar com que suas funções embarcadas façam parte do trabalho, o pacote conta com diversos recursos para derivação, integração, interpolação, trigonometria e muitos outros.

Vale destacar que no momento não conheço nenhuma função NumPy que calcule a derivada segunda em um arranjo. De qualquer maneira, se admitirmos que a derivada segunda pode ser aproximada com a aplicação dupla da derivada primeira (lembre-se que embora analiticamente sejam equivalentes, numericamente isso nem sempre é verdade), podemos usar a função np.gradient para reescrever nosso código na forma:

%%timeit
for n in range(t.size-1):
    T[:,:,n+1] = T[:,:,n] + dt * alpha * (
        np.gradient(np.gradient(T[:,:,n], x, axis=0), x, axis=0) +
        np.gradient(np.gradient(T[:,:,n], y, axis=1), y, axis=1)
    )
    # Condições de contorno
    T[0,:,n+1], T[-1,:,n+1], T[:,0,n+1], T[:,-1,n+1] = Tx0, Txn, Ty0, Tyn

221 ms ± 43.2 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

A figura dos resultados mais uma vez:

minha_figura(T, x, y)

Essa abordagem pode não ser tão precisa quanto as que vimos anteriormente, mas a descrição de como implementar operadores diferenciais será assunto para um outro dia. Por outro lado, se ainda assim e erro está em uma faixa tolerável para a sua aplicação, essa pode ser uma alternativa pela facilidade de aplicação e boa legibilidade do código. Como qualquer outro arranjo NumPy, devemos lembrar de que definimos a temperatura na ordem [x, y e t], e assim, axis=0 resultará no gradiente na direção x, enquanto axis=1 será o gradiente em y.

Xarray

Uma vez realizada a contextualização, vamos agora abordar a transferência de calor transiente bidimensional com Xarray, um pacote para estruturas de dados rotulados N-dimensionais (também denominados tensores). A sua vantagem é permitir realizar operações empregando o nome das coordenadas em vez da sua numeração (dim='x' em vez de axis=0), além de armazenar atributos como o nome e unidade das diversas variáveis.

O ganho imediato em usar Xarray é que escrevemos menos código. A longo prazo o ganho é a legibilidade, podemos entender o que estávamos pensando ao retomar para um código semanas ou meses depois.

Para exemplificar, vamos iniciar criando um Dataset para armazenar as informações do nosso problema. Existem diversos modos para isso, e uma leitura na documentação oficial é recomendada. Com o seguinte bloco de código, inicializamos nosso sistema de coordenadas:

data = xr.Dataset(coords={
    'x': np.linspace(start = 0., stop = 0.5, num = 21, endpoint = True),
    'y': np.linspace(start = 0., stop = 0.5, num = 21, endpoint = True),
    't': np.linspace(start = 0., stop = 600., num = 601, endpoint = True)
})

Ao contrário do exemplo anterior em Numpy onde tínhamos as três variáveis (x, y e t), aqui toda a informação está consolidada em uma única estrutura, que denominamos data. O acesso específico a cada uma delas ocorre de maneira similar a notação dos dicionários em Python, isso é, data['x'], ou ainda de maneira mais condensada como data.x, por exemplo.

Vamos adicionar atributos às nossas coordenadas para facilitar o entendimento do código, além disso, veremos que os atributos são automaticamente incluídos nas figuras, diminuindo nosso trabalho futuro. Aqui incluimos as unidades e denominamos t como tempo:

data.x.attrs['units'] = 'm'
data.y.attrs['units'] = 'm'
data.t.attrs['units'] = 's'
data.t.attrs['name'] = 'tempo'

Agora definimos a temperatura como um arranjo tridimensional (x, y e tempo) e também incluimos os atributos para referência:

data['T'] = xr.DataArray(0., coords=[data.x, data.y, data.t])

data.T.attrs['units'] = '°C'
data.T.attrs['name'] = 'Temperatura'

E as propriedades do material:

data['alpha'] = 1.407e-5

data.alpha.attrs['units'] = r'm$^2$/s'
data.alpha.attrs['name'] = 'Difusividade térmica'

Em um ambiente Jupyter Notebook interativo, visualizamos facilmente todo o conteúdo e atributos da nossa estrutura de dados ao imprimi-la na tela:

data

<xarray.Dataset>
Dimensions:  (t: 601, x: 21, y: 21)
Coordinates:



x        (x) float64 0.0 0.025 0.05 0.075 0.1 … 0.4 0.425 0.45 0.475 0.5


y        (y) float64 0.0 0.025 0.05 0.075 0.1 … 0.4 0.425 0.45 0.475 0.5


t        (t) float64 0.0 1.0 2.0 3.0 4.0 … 596.0 597.0 598.0 599.0 600.0
Data variables:
T        (x, y, t) float64 0.0 0.0 0.0 0.0 0.0 0.0 … 0.0 0.0 0.0 0.0 0.0
alpha    float64 1.407e-05

Existe uma série de métodos para selecionar dados dentro dos nossos arranjos (mais informações aqui), uma delas é por meio de dicionários. Por exemplo, para impor a condição inicial na temperatura podemos usar o dicionário {'t' : 0}, ou a notação equivalente dict(t=0). De maneira análoga, iremos impor as condições de contorno, como vemos:

# Condição Inicial
data.T[dict(t=0)] = T0

# Condições de Contorno
data.T[dict(t=0,x=0)] = (Td - Ta) / (data.y[-1] - data.y[0]) * data.y + Ta
data.T[dict(t=0,x=-1)] = (Tb - Tc) / (data.y[-1] - data.y[0]) * data.y + Tc
data.T[dict(t=0,y=0)] = (Tc - Ta) / (data.x[-1] - data.x[0]) * data.x + Ta
data.T[dict(t=0,y=-1)] = (Tb - Td) / (data.x[-1] - data.x[0]) * data.x + Td

Se novamente admitirmos que a derivada segunda pode ser aproximada com a aplicação dupla da derivada primeira, resolvemos o problema com o seguinte bloco de código:

%%time
for n in range(data.t.size - 1):
    dt = data.t[n+1] - data.t[n]
    # Equação Governate
    data.T[dict(t=n+1)] = data.T.isel(t=n) + dt * data.alpha * (
        data.T.isel(t=n).differentiate('x').differentiate('x') +
        data.T.isel(t=n).differentiate('y').differentiate('y')
    )
    # Condições de Contorno
    data.T[dict(t=n+1,x=0)] = data.T.isel(t=0,x=0)
    data.T[dict(t=n+1,x=-1)] = data.T.isel(t=0,x=-1)
    data.T[dict(t=n+1,y=0)] = data.T.isel(t=0,y=0)
    data.T[dict(t=n+1,y=-1)] = data.T.isel(t=0,y=-1)

Wall time: 5.2 s

Note a diferença visual em relação ao nosso exemplo anterior em NumPy, onde sempre temos que lembrar da ordem de definição dos eixos para manipular os dados, como np.gradient(T[:,:,n], x, axis=0) para derivação da temperatura no tempo n em relação a x, com Xarray usamos simplesmente data.T.isel(t=n).differentiate('x').

Outra vantagem de usar Xarray, o pacote oferece uma série de funcionalidades gráficas, construídas sobre Matplotlib (mais informações aqui), de modo que com poucas linhas de código podemos:

# Graficar a evolução temporal da temperatura no centro da placa
data.T.isel(x=data.x.size//2, y=data.y.size//2).plot.line();

# Variação com x e t para y fixo
data.T.isel(t=slice(None,None,120), y=data.y.size//2).plot.line(x='x');

# Variação com y e t para x fixo
data.T.isel(t=slice(None,None,120), x=data.x.size//2).plot.line(x='y');

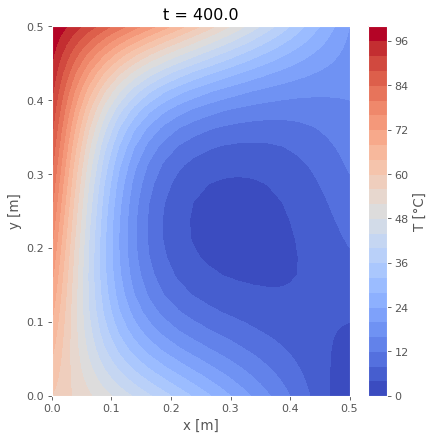
# E aqui temos a completa variação espaço-temporal
data.T.sel(t=slice(None,None,40)).T.plot.contourf(
    col='t',
    col_wrap=4,
    aspect = 1,
    cmap='bone',
    levels = 32
);

Conclusão

Com esse estudo de caso, demonstrou-se como resolver a condução de calor em placa plana bidimensional transiente empregando dois diferentes pacotes para manipulação de arranjos, NumPy e Xarray. Vimos como o primeiro funciona baseado na numeração dos diferentes eixos de coordenadas axis=0, enquanto o segundo utiliza rótulos dim='x', em uma apresentação muito mais intuitiva e visual. Certamente, cada abordagem tem seus pontos fortes e fracos, e a escolha de uma ou outra depende do tipo de aplicação em questão e da preferência do próprio programador.