Integração numérica com a Regra dos Trapézios

Introdução

A operação integral é, de maneira geral, representada pela seguinte equação: \[ \int_a^b f(x)dx. \]

No contexto geométrico, essa operação é capaz de calcular a área sob a curva \( f(x) \), para o intervalo \( a \le x \le b \). Muitas das funções mais conhecidas apresentam uma integral definida, isso é, podem ser calculadas de forma analítica, e essas definições aparecem em Tabelas de Integrais ou em utilitários de álgebra simbólica (SymPy, por exemplo).

Existem casos onde a solução analítica não é possível, já que a função é de elevada complexidade ou mesmo desconhecida, e aí podemos recorrer aos métodos numéricos.

Trapézio Simples

A regra do trapézio é uma das primeiras técnicas de integração que aprendemos em um curso de métodos numéricos. Ela consiste em aproximar a área sob a curva da função \( f(x) \) como a área de um trapézio, dada pela equação:

\[ \int_a^b f(x)dx \approx \dfrac{f(a) + f(b)}{2} (b-a). \]

O que seria o equivalente a calcular a área demarcada pela região azul na figura:

Considerando a função \( f(x) = \cos(x) + x/\pi \) no intervalo \( 0 \le x \le 4 \pi \), podemos facilmente calcular o valor da integral pelo método do trapézio como:

\[ \int_0^{4 \pi} f(x)dx \approx \dfrac{1 + 5}{2} (4\pi-0) \approx 37,699. \]

Sabe-se, entretanto, que a solução exata é aproximadamente \( 25,133 \). Nossa estimativa passou longe do valor esperado, mas como podemos melhorar isso?

Trapézio Composto

Bem, podemos melhorar a aproximação para o cálculo do valor da integral ao aumentarmos o número de trapézios, ou ao usar a regra trapezoidal composta. Ela é dada pela equação:

\[ \int_a^b fdx \approx \sum_{i=0}^{n-1} \dfrac{f_{i} + f_{i+1}}{2} \Delta x = \dfrac{\Delta x}{2} \left( f_1 + 2f_2 + \dots + 2f_{n-1} + f_{n}\right). \]

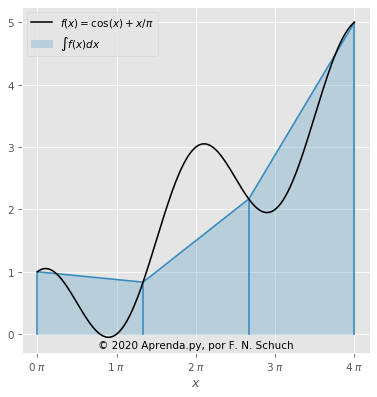
Vamos considerar a mesma função \( f(x) = \cos(x) + x/\pi \) no intervalo \( 0 \le x \le 4 \pi \). Se considerarmos \( n = 4 \), a integral vai representar a área azul na figura:

Melhor, não? Calcular seu valor já não é tão trivial, mas que tal começarmos a por a mão na massa?

import numpy as np # Importamos nossa biblioteca preferida

def f(x): # Transcrevemos a função dada
    return np.cos(x) + x/np.pi

dx = 4*np.pi/3 # Calculamos o dx para esse caso

# E finalmente calculamos a integral
# pelo método trapezoidal composto
dx*(f(0*dx) + 2*f(1*dx) + 2*f(2*dx) + f(3*dx))/2

    25.132741228718345

A resposta chegou mais perto. Podemos continuar aumentando o número de pontos empregados para diminuir o erro. Mas mais pontos demandariam muito trabalho com a abordagem que usamos aqui, a equação nem caberia na tela. Vamos automatizar esse processo?

Implementação

Vamos resolver o método trapezoidal para a mesma função e intervalo, mas agora com ainda mais pontos, que tal \( n = 21 \)? A representação visual é essa:

Vamos ir aumentando o nível de requinte do código, para que ele faça todo o trabalho dessa vez:

# Aqui definimos o intervalo que queremos,
# bem como o número de pontos
x = np.linspace(0, 4*np.pi, num=21)

'''
E é tudo que precisamos,
o resto é por conta do computador
'''

y = f(x) # Nossa função já foi definida no bloco anterior

dx = x[1] - x[0] # Obtém o espaçamento

I = 0. # A operação envolve um somatório, então iniciamos uma variável acumuladora

I += dx*y[0]/2

for i in range(1,x.size-1): # Reflita, por que esse laço vai de 1 até n-1?
    I += dx*y[i]

I += dx*y[-1]/2

print(I) # E finalmente temos o resultado

    25.132741228718345

E estamos cada vez mais perto da resposta exata. Nesse ponto, se estiver seguindo essa lição com uma aplicação Python aberta (o que é altamente recomendado), aproveite para experimentar diferentes possibilidades, varie os parâmetros, varie a função, veja o que acontece.

Operador Integral

Após se divertir com os códigos que criamos até aqui, vamos prosseguir nossa escalada no que se refere a elegância. Vamos apresentar nossa integral na forma de um operador integral. Retorne até a equação da regra trapezoidal composta e dê uma boa olhada. Percebe o padrão? Todos os termos são multiplicados por \( \Delta x \), com exceção do primeiro e do último, que são multiplicados por \( \Delta x / 2 \). Ora, se isso não tem exatamente a aparência de um vetor preenchido pelo valor 1, onde o primeiro e último elemento são divididos por 2, e então todos multiplicados por \( \Delta x \), e por fim somados. São muitas palavras, mas não se assuste, a aparência não é tão ruim:

\[ \int_a^b f(x) dx = \sum_{i=1}^n \big( W_i f(x_i) \big), \] sendo o operador integral dado por \[ W = \Delta x [ 1/2, 1, \dots, 1, \dots, 1, 1/2 ]. \]

Tendo em vista que a coordenada x, a função y e o espaçamento da malha dx já foram todos definidos nos blocos anteriores, tudo que precisamos agora é definir o nosso operador integral:

# Iniciamos o operador integral como um vetor
# preenchido por 1, multiplicado por dx
W = dx*np.ones_like(x)

# Dividimos o primeiro e último elemento por 2
for i in [0, -1]:
    W[i] /= 2.0

# A multiplicação do operador pela função e a
# soma dos elementos fornece nossa resposta
np.sum(W * y)

    25.132741228718345

Nessa opção, após a inicialização, podemos calcular outras integrais apenas repetindo a última linha do código, aumentando a legibilidade e a chance de reutilização do código, e menos linhas para copiar e colar também são um benefício na hora de procurar e corrigir falhas.

Biblioteca SciPy

Meus parabéns se você chegou até aqui, o último passo. Vamos recapitular, já vimos quatro maneiras diferentes para calcular uma integral:

1. Com a regra simples, a resposta veio de uma simples continha;
2. Ao passar para a regra composta as coisas cresceram, usamos uma calculadora;
3. Vimos como automatizar o cálculo, e foi então possível experimentar diversas combinações de parâmetros;
4. Então, aumentamos a elegância e resolvemos o problema de forma matricial.

Agora, a última etapa envolve um dos motivos pelo qual Python tem se tornado tão popular: existe uma infinidade de bibliotecas já programadas, prontas para realizar diversas tarefas. De modo que podemos fazer:

from scipy.integrate import trapz
trapz(y,x)

    25.132741228718345

Lindo, não? Repare que obtivemos exatamente a mesma resposta para os três últimos exercícios, mostrando que existem diferentes caminhos a serem trilhados. A prática vai lhe permitir escolher entre eles.

Fazemos um destaque à função scipy.integrate.cumtrapz, que calcula a integral de forma acumulativa, que pode ser particularmente útil dependendo da aplicação.

Exemplos

# Um exemplo unidirecional
trapz([1,2,3])

    4.0

# Onde podemos informar como argumento
# opcional o sistema de coordenadas
trapz([1,2,3], x=[4,6,8])

    8.0

# Ou o espaçamento dos pontos,
# caso seja uniforme
trapz([1,2,3], dx=2)

    8.0

# Esse é o exemplo de um caso bidimensional
a = np.arange(6).reshape(2, 3)
a

    array([[0, 1, 2],
           [3, 4, 5]])

# Integral em x
trapz(a, axis=0)

    array([1.5, 2.5, 3.5])

# Integral em y
trapz(a, axis=1)

    array([2., 8.])

# Integral dupla: x e então em y
trapz(trapz(a, axis=0), axis=0)

    5.0

# Integral dupla: y e então em x
trapz(trapz(a, axis=-1), axis=-1)

    5.0

Bônus: Erro do método

Por fim, podemos ver que o erro do método numérico decresce exponencialmente, na ordem de \( n^{-2} \), em função do aumento do número de pontos:

Mas ele fica saturado por volta de \( 10^{-12} \). É hora da reflexão, você sabe me dizer o que acontece ali?